Complete Distance Calculator Guide: Master Distance Calculations
Introduction: The Science of Measuring Space
Distance calculation is fundamental to mathematics, science, engineering, and everyday life. Whether measuring the shortest path between two points, calculating travel distances on Earth, or determining spatial relationships in 3D designs, accurate distance calculations are essential. Our Distance Calculator makes these calculations effortless, providing accurate results with visual representations and step-by-step explanations.
This guide will teach you:
- Four different distance calculation methods
- Mathematical formulas and their derivations
- Real-world applications across industries
- How to use our calculator effectively
- Tips for accurate measurements and calculations
Ready to calculate? Use our Distance Calculator for comprehensive distance calculations with visualizations.
📖 Table of Contents
- Distance: The Foundation of Spatial Measurement
- Four Calculation Modes Explained
- 2D Distance: Euclidean Plane Calculations
- 3D Distance: Spatial Measurements
- Geographic Distance: Earth's Surface Calculations
- Multi-Point Distance: Path and Route Planning
- Distance Calculator: Step-by-Step Guide
- Interactive Visualization Features
- Mathematical Formulas and Derivations
- Real-World Applications
- Common Distance Calculation Mistakes
- Measurement Units and Conversions
- Coordinate Systems Explained
- Related Distance Concepts
- Educational Benefits
- Professional Uses
- FAQs: Your Distance Questions Answered
- Practice Problems with Solutions
1️⃣ Distance: The Foundation of Spatial Measurement
What Is Distance?
Definition: The measure of separation between two points in space Key properties:
- Always positive or zero
- Symmetric (distance A→B = distance B→A)
- Follows triangle inequality
- Measurable in various units
Why Distance Matters
Everyday applications:
- Navigation and travel planning
- Construction and design
- Sports and athletics
- Shopping and logistics
- Social distancing
Scientific importance:
- Physics and motion studies
- Astronomy and cosmology
- Geography and cartography
- Engineering and architecture
- Computer graphics and gaming
Distance vs. Displacement
Distance: Total path length traveled Displacement: Straight-line distance from start to end Our calculator handles both concepts effectively
Historical Context
Ancient measurements:
- Egyptian cubits
- Roman miles
- Greek stadia
- Chinese li
Modern standardization:
- Metric system (1795)
- International System of Units (1960)
- GPS precision (1990s-present)
2️⃣ Four Calculation Modes Explained
Multiple Calculation Approaches
Our calculator offers 4 modes:
- 2D Distance: Points in a plane (x, y)
- 3D Distance: Points in space (x, y, z)
- Geographic Distance: Earth coordinates (lat, lon)
- Multi-Point Distance: Path along multiple points
Mode Selection Guide
Choose based on your needs:
- 2D Mode: Flat surfaces, maps, diagrams
- 3D Mode: Architecture, 3D modeling, physics
- Geographic Mode: Navigation, travel, surveying
- Multi-Point Mode: Routes, perimeters, complex paths
Input Requirements
Each mode requires different inputs:
- 2D: x₁, y₁, x₂, y₂
- 3D: x₁, y₁, z₁, x₂, y₂, z₂
- Geographic: lat₁, lon₁, lat₂, lon₂
- Multi-Point: Series of (x, y) points
Input Validation
The tool checks:
- Valid numerical inputs
- Geographic coordinate ranges
- Minimum point requirements
- Mathematical validity
Prevents common errors in calculations.
3️⃣ 2D Distance: Euclidean Plane Calculations
What Is 2D Distance?
Definition: Straight-line distance between two points in a plane Formula: d = √[(x₂ - x₁)² + (y₂ - y₁)²] Also known as: Euclidean distance, Cartesian distance
Mathematical Foundation
Pythagorean Theorem application:
For right triangle with sides a and b:
c² = a² + b²
c = √(a² + b²)
Applied to coordinates:
Δx = x₂ - x₁ (horizontal difference)
Δy = y₂ - y₁ (vertical difference)
d = √(Δx² + Δy²)
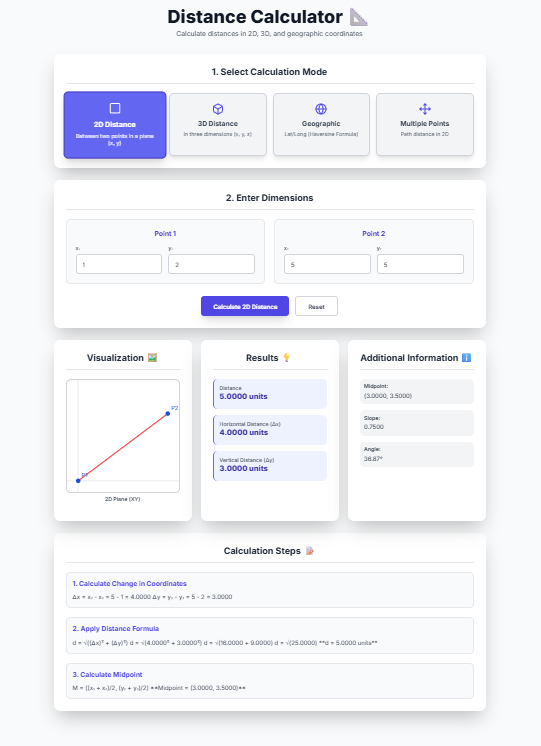
Example Calculation
Given points: P₁(1, 2) and P₂(5, 5)
Δx = 5 - 1 = 4
Δy = 5 - 2 = 3
d = √(4² + 3²) = √(16 + 9) = √25 = 5 units
Additional 2D Calculations
Midpoint:
M = ((x₁ + x₂)/2, (y₁ + y₂)/2)
Slope:
m = (y₂ - y₁)/(x₂ - x₁)
Angle from horizontal:
θ = arctan(Δy/Δx)
Real-World 2D Applications
Common uses:
- Map distances on flat projections
- Screen coordinates in computer graphics
- Fabric cutting patterns
- Floor planning
- Sports field measurements
Using 2D Mode in the Tool
Visualization shows:
- Two points on coordinate plane
- Connecting line segment
- Distance measurement
- Coordinate grid reference
Step-by-step display includes formula application.
4️⃣ 3D Distance: Spatial Measurements
What Is 3D Distance?
Definition: Straight-line distance between two points in three-dimensional space Formula: d = √[(x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²] Extension of: 2D Pythagorean theorem
Mathematical Derivation
Three-dimensional Pythagorean theorem:
d² = Δx² + Δy² + Δz²
d = √(Δx² + Δy² + Δz²)
Coordinate differences:
Δx = x₂ - x₁
Δy = y₂ - y₁
Δz = z₂ - z₁
Example Calculation
Given points: P₁(0, 0, 0) and P₂(3, 4, 12)
Δx = 3 - 0 = 3
Δy = 4 - 0 = 4
Δz = 12 - 0 = 12
d = √(3² + 4² + 12²) = √(9 + 16 + 144) = √169 = 13 units
Additional 3D Calculations
Midpoint:
M = ((x₁ + x₂)/2, (y₁ + y₂)/2, (z₁ + z₂)/2)
2D Projection: Distance ignoring z-coordinate Volume diagonal calculations Spatial relationships in 3D models
Real-World 3D Applications
Common uses:
- Architecture and building design
- 3D printing and modeling
- Physics and engineering
- Computer-aided design (CAD)
- Virtual reality environments
- Drone flight planning
3D Visualization Challenges
The interface shows XY-plane projection Z-axis represented numerically Helps understand spatial relationships
Special 3D Cases
Points in same vertical line: Δx = 0, Δy = 0 Points in same horizontal plane: Δz = 0 The tool handles all cases correctly
5️⃣ Geographic Distance: Earth's Surface Calculations
What Is Geographic Distance?
Definition: Great-circle distance between two points on Earth's surface Formula: Haversine formula Earth model: Sphere with radius ≈ 6,371 km
The Haversine Formula
Mathematical formula:
a = sin²(Δφ/2) + cos φ₁ × cos φ₂ × sin²(Δλ/2)
c = 2 × atan2(√a, √(1−a))
d = R × c
Where:
- φ = latitude in radians
- λ = longitude in radians
- Δφ = φ₂ − φ₁
- Δλ = λ₂ − λ₁
- R = Earth's radius (≈6,371 km)
Why Great-Circle Distance?
Shortest path on sphere surface Follows Earth's curvature Used in aviation and navigation More accurate than flat approximations
Example Calculation
Given locations:
- New York: 40.7128° N, 74.0060° W
- Los Angeles: 34.0522° N, 118.2437° W
Convert to radians:
φ₁ = 40.7128 × π/180 ≈ 0.7106
λ₁ = -74.0060 × π/180 ≈ -1.2916
φ₂ = 34.0522 × π/180 ≈ 0.5944
λ₂ = -118.2437 × π/180 ≈ -2.0641
Calculate:
Δφ = -0.1162
Δλ = -0.7725
a = sin²(-0.1162/2) + cos(0.7106)×cos(0.5944)×sin²(-0.7725/2) ≈ 0.1668
c = 2 × atan2(√0.1668, √0.8332) ≈ 0.8185
d = 6371 × 0.8185 ≈ 5,217 km
Real-World Geographic Applications
Common uses:
- Airline flight planning
- Shipping route optimization
- GPS navigation systems
- Geographic information systems (GIS)
- Sports event planning (marathons, races)
- Telecommunications (signal coverage)
Accuracy Considerations
Earth is not perfect sphere:
- Equatorial radius: 6,378.1 km
- Polar radius: 6,356.8 km
- WGS-84 ellipsoid model more accurate The tool uses mean radius for simplicity
Bearing Calculation
Initial bearing formula:
θ = atan2(sin Δλ × cos φ₂, cos φ₁ × sin φ₂ − sin φ₁ × cos φ₂ × cos Δλ)
Additionally, you get bearing information
6️⃣ Multi-Point Distance: Path and Route Planning
What Is Multi-Point Distance?
Definition: Total distance along path connecting multiple points Calculation: Sum of distances between consecutive points Also called: Path length, route distance, perimeter
Mathematical Approach
For n points P₁, P₂, ..., Pₙ:
Total distance = Σ d(Pᵢ, Pᵢ₊₁) for i = 1 to n-1
Where d(Pᵢ, Pᵢ₊₁) = √[(xᵢ₊₁ - xᵢ)² + (yᵢ₊₁ - yᵢ)²]
Example Calculation
Given points:
- P₁(0, 0)
- P₂(3, 4)
- P₃(6, 0)
Calculate segments:
d₁₂ = √[(3-0)² + (4-0)²] = √(9 + 16) = √25 = 5
d₂₃ = √[(6-3)² + (0-4)²] = √(9 + 16) = √25 = 5
Total = 5 + 5 = 10 units
Path vs. Straight-Line Distance
Path distance: Actual travel distance along route Straight-line distance: Direct distance from start to end Path ≥ Straight-line (triangle inequality)
Real-World Multi-Point Applications
Common uses:
- Road trip planning
- Delivery route optimization
- Hiking trail measurement
- Surveying property boundaries
- Robotics path planning
- Sports track design
- Pipeline or cable routing
Efficiency Considerations
Traveling Salesman Problem: Finding shortest route visiting all points The tool calculates given order only Visualization shows complete path
Advanced Features
Segment-by-segment breakdown Average segment length Total segments count All these metrics are provided
7️⃣ Distance Calculator: Step-by-Step Guide
Mode Selection Interface
Four colorful mode cards:
- 2D Distance (Square icon): Pink selection
- 3D Distance (Box icon): Green selection
- Geographic Distance (Globe icon): Blue selection
- Multi-Point Distance (Move icon): Yellow selection
Input Entry Process
For single-point modes (2D, 3D, Geographic):
- Point 1 and Point 2 input sections
- Clearly labeled coordinate fields
- Validation for geographic ranges
- Step values for precision control
For Multi-Point mode:
- Dynamic point list with add/remove buttons
- Each point has x and y inputs
- Minimum 2 points required
- Clear visual labeling (P1, P2, etc.)
Calculation Execution
Click "Calculate" button:
- Input validation occurs
- Appropriate calculation runs
- Results populate instantly
- Visualization updates
- Page scrolls to results
Results Presentation
Four result sections:
- Visualization: Interactive diagram of points and distances
- Results: Primary distance measurements
- Additional Information: Supplementary calculations
- Calculation Steps: Detailed mathematical derivation
Reset Functionality
Soft reset: Clears current inputs Maintains mode selection Ready for new calculation Preserves default examples
Error Handling
Input validation: Prevents invalid calculations Clear error messages: Explain what went wrong Graceful recovery: Suggestions for correction Toast notifications: Non-disruptive alerts
8️⃣ Interactive Visualization Features
Dynamic Visual Representations
Each mode has tailored visualization:
- 2D Mode: Coordinate plane with points and connecting line
- 3D Mode: XY-plane projection with z-values noted
- Geographic Mode: Simplified map projection
- Multi-Point Mode: Complete path with all points connected
Visualization Elements
Common features across modes:
- Points labeled P1, P2, etc.
- Distance lines in red
- Coordinate axes when applicable
- Scale adaptation to input values
- Clean, uncluttered presentation
Educational Value
Visual learning benefits:
- Understand spatial relationships
- Verify calculation results
- See coordinate system application
- Build geometric intuition
Professional Utility
Design verification:
- Check spatial arrangements
- Validate measurements
- Communicate designs visually
- Present results clearly
Responsive Design
Works on all devices:
- Desktop computers
- Tablets and laptops
- Smartphones
- Different screen sizes
Visualization adapts to available space.
Technical Implementation
SVG-based rendering for sharp graphics Dynamic scaling to fit data range Real-time updates with calculations Accessible design with clear labels
9️⃣ Mathematical Formulas and Derivations
Euclidean Distance Formula
General n-dimensional formula:
d = √[Σ (pᵢ - qᵢ)²] for i = 1 to n
Where:
- p, q are n-dimensional points
- pᵢ, qᵢ are coordinate components
Pythagorean Theorem Foundation
Right triangle relationship:
c² = a² + b²
Extended to n dimensions:
d² = Δ₁² + Δ₂² + ... + Δₙ²
Haversine Formula Derivation
Spherical law of cosines alternative:
d = R × arccos(sin φ₁ sin φ₂ + cos φ₁ cos φ₂ cos Δλ)
Numerical stability issues led to haversine formula Haversine function: hav(θ) = sin²(θ/2)
Conversion Formulas
Degrees to radians:
radians = degrees × π/180
Radians to degrees:
degrees = radians × 180/π
Coordinate Transformation
Cartesian to polar:
r = √(x² + y²)
θ = arctan(y/x)
Polar to Cartesian:
x = r cos θ
y = r sin θ
Precision Handling
High-precision calculations:
- Double-precision floating point
- Accurate trigonometric functions
- Careful rounding only at display
- Consistent unit handling
🔟 Real-World Applications
Transportation and Logistics
Route optimization:
- Delivery truck routing
- Airline flight planning
- Shipping container logistics
- Public transportation planning
Infrastructure planning:
- Road and highway design
- Railway route planning
- Pipeline network design
- Power line placement
Construction and Engineering
Building design:
- Structural component placement
- Utility line installation
- Surveying and land measurement
- Material quantity estimation
Civil engineering:
- Bridge design and placement
- Tunnel alignment
- Dam construction planning
- Urban development planning
Technology and Computing
Computer graphics:
- 3D rendering and animation
- Game development
- Virtual reality environments
- Augmented reality applications
Geographic information systems:
- Map creation and analysis
- Environmental monitoring
- Urban planning
- Disaster response planning
Science and Research
Physics and astronomy:
- Planetary motion calculations
- Particle physics trajectories
- Cosmological distance measurements
- Experimental setup design
Biology and ecology:
- Animal migration patterns
- Plant distribution studies
- Habitat connectivity analysis
- Environmental impact assessment
Everyday Life Applications
Personal navigation:
- GPS driving directions
- Hiking and outdoor activities
- Real estate property measurement
- Sports and fitness tracking
Home and garden:
- Furniture arrangement
- Garden layout planning
- Home renovation measurements
- Decor placement optimization
Using the Tool Professionally
Save time on repetitive calculations Reduce errors in manual computations Document calculations with steps Share visualizations with clients or teams Train employees with interactive examples
1️⃣1️⃣ Common Distance Calculation Mistakes
Mistake 1: Unit Inconsistency
Mixing different units in one calculation Solution: Use consistent units throughout
Mistake 2: Coordinate System Confusion
Using geographic coordinates as Cartesian Solution: Understand coordinate system differences
Mistake 3: Early Rounding
Rounding intermediate values losing precision Solution: Maintain full precision until final result
Mistake 4: Formula Misapplication
Using 2D formula for geographic distances Solution: Choose appropriate formula for context
Mistake 5: Sign Errors
Ignoring negative coordinates or differences Solution: Pay attention to signs in calculations
Mistake 6: Earth Model Simplification
Treating Earth as flat for long distances Solution: Use spherical calculations for >20 km
Mistake 7: Point Order Assumption
Assuming specific point order in multi-point Solution: Verify point sequence matches path
Built-in Safeguards
The tool prevents these through:
- Unit consistency enforcement
- Coordinate validation
- Full precision maintenance
- Formula auto-selection
- Sign handling
- Earth curvature consideration
- Clear point labeling
Still, understand the underlying concepts.
1️⃣2️⃣ Measurement Units and Conversions
Common Distance Units
Metric System:
- Millimeter (mm): 0.001 m
- Centimeter (cm): 0.01 m
- Meter (m): Base unit
- Kilometer (km): 1,000 m
Imperial System:
- Inch (in): 1/12 ft
- Foot (ft): Base unit
- Yard (yd): 3 ft
- Mile (mi): 5,280 ft
Specialized Units
Nautical:
- Nautical mile: 1,852 m (1 minute of latitude)
- Knot: Nautical mile per hour
Astronomical:
- Astronomical unit (AU): Earth-Sun distance
- Light-year: Distance light travels in one year
- Parsec: 3.26 light-years
Conversion Factors
Common conversions:
1 m = 3.28084 ft
1 ft = 0.3048 m
1 km = 0.621371 mi
1 mi = 1.60934 km
1 nautical mile = 1.15078 mi
Unit Selection Strategy
Choose based on:
- Industry standards
- Measurement tools available
- Required precision
- Personal preference
- International compatibility
The calculator works with any consistent units.
Precision Requirements
Different applications need different precision:
- Surveying: Millimeter precision
- Construction: Centimeter precision
- Navigation: Meter precision
- Astronomy: Kilometer precision or greater
The interface provides high precision for all needs.
Unit Conversion Best Practices
Always document original units Convert systematically using established factors Double-check critical conversions Use standard conversion tools when possible
1️⃣3️⃣ Coordinate Systems Explained
Cartesian Coordinate System
Two-dimensional (2D):
- x-axis (horizontal)
- y-axis (vertical)
- Origin (0, 0)
- Quadrants I-IV
Three-dimensional (3D):
- x, y, z axes
- Right-hand rule
- Octants
- 3D space partitioning
Geographic Coordinate System
Latitude (φ):
- Measures north-south position
- Range: -90° to 90°
- Equator: 0°
- Poles: ±90°
Longitude (λ):
- Measures east-west position
- Range: -180° to 180°
- Prime meridian: 0°
- International Date Line: ±180°
Polar Coordinate System
Two-dimensional:
- Radius (r): Distance from origin
- Angle (θ): Direction from reference
- Conversion to Cartesian: x = r cos θ, y = r sin θ
Other Coordinate Systems
Cylindrical coordinates: (r, θ, z) Spherical coordinates: (ρ, θ, φ) Projected coordinates: Map projections
Coordinate System Selection
Choose based on:
- Problem symmetry
- Measurement methods
- Calculation simplicity
- Industry standards
The tool handles Cartesian and geographic systems.
Coordinate Transformations
Conversion between systems often necessary Internal processing manages transformations Users input in natural coordinate system
1️⃣4️⃣ Related Distance Concepts
Manhattan Distance
Also called: Taxicab distance, L1 distance Formula: d = |x₂ - x₁| + |y₂ - y₁| Application: Grid-based navigation
Chebyshev Distance
Also called: Chessboard distance, L∞ distance Formula: d = max(|x₂ - x₁|, |y₂ - y₁|) Application: King's moves in chess
Minkowski Distance
Generalized distance:
d = (Σ |pᵢ - qᵢ|^p)^(1/p)
Special cases:
- p=1: Manhattan distance
- p=2: Euclidean distance
- p=∞: Chebyshev distance
Mahalanobis Distance
Statistical distance measure Accounts for covariance between variables Useful in pattern recognition
Hamming Distance
For string or sequence comparison Counts differing positions Applications in coding theory, genetics
Edit Distance
Also called: Levenshtein distance Measures string similarity Minimum edits to transform one string to another
Primary Focus
Concentrates on: Euclidean distances Most practical applications Clear visualization possible Educational value highest
1️⃣5️⃣ Educational Benefits
Learning Geometry Concepts
Visual understanding:
- Coordinate system operation
- Distance formula application
- Spatial relationship visualization
- Measurement unit comprehension
Interactive visualization enhances geometric learning.
Mathematical Skill Development
Formula application practice:
- Input values into formulas
- Step-by-step calculation
- Result verification
- Error checking
Active learning vs. rote memorization.
Problem-Solving Skills
Develops systematic approach:
- Problem analysis
- Method selection
- Calculation execution
- Result interpretation
- Verification procedures
Real context makes math meaningful.
Multiple Learning Styles
Accommodates diverse learners:
- Visual: Diagrams and colors
- Auditory: Step explanations
- Kinesthetic: Interactive inputs
- Reading/writing: Detailed text
Serves all learning preferences.
Homework Assistance
Check work effectively:
- Verify calculations
- Understand mistakes
- Learn correct approach
- Build confidence
Educational tool, not shortcut.
Test Preparation
Practice problems:
- Various coordinate systems
- Different distance types
- Real-world scenarios
- Timed practice sessions
Build fluency with calculations.
Teacher Resource
Create lessons with interactive examples Demonstrate concepts visually Generate practice problems Show real applications
Enhance classroom teaching effectiveness.
1️⃣6️⃣ Professional Uses
Engineering Fields
Mechanical engineering:
- Machine component placement
- Tolerance analysis
- Assembly line design
- Robotics positioning
Civil engineering:
- Structure alignment
- Road grade calculations
- Surveying measurements
- Construction planning
Electrical engineering:
- Circuit board layout
- Transmission line planning
- Antenna placement
- Signal propagation analysis
Architecture and Design
Building design:
- Room dimensions
- Furniture layout
- Lighting placement
- Accessibility compliance
Urban planning:
- Park and green space design
- Transportation network planning
- Utility infrastructure
- Zoning compliance
Technology Industry
Software development:
- Game physics engines
- Mapping applications
- Augmented reality
- Data visualization
Data science:
- Cluster analysis
- Pattern recognition
- Geographic analysis
- Machine learning features
Scientific Research
Physics research:
- Experimental setup design
- Particle trajectory analysis
- Cosmological measurements
- Material science studies
Environmental science:
- Habitat fragmentation analysis
- Species distribution modeling
- Pollution dispersion studies
- Climate change impact assessment
Professional Application Tips
Save time on repetitive calculations Reduce errors in critical work Document calculations for reference Share results with colleagues or clients Train team members with consistent tool
❓ Frequently Asked Questions
Q: How accurate is the distance calculator? A: The tool uses double-precision floating-point arithmetic, providing accuracy to about 15 decimal places. For geographic calculations, it uses Earth's mean radius of 6,371 km. This is more than sufficient for most practical applications. The limiting factor is usually the accuracy of your input measurements, not the calculator's precision.
Q: Can I calculate distance with negative coordinates? A: Yes! Negative coordinates work perfectly in all modes. In 2D and 3D modes, negative values simply indicate positions left of or below the origin. In geographic mode, negative latitudes indicate southern hemisphere, and negative longitudes indicate western hemisphere.
Q: What's the difference between 2D and 3D distance calculations? A: 2D distance calculates the straight-line distance in a plane (ignoring height differences), while 3D distance includes vertical differences. The formulas are: 2D: d = √[(x₂-x₁)² + (y₂-y₁)²], 3D: d = √[(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²].
Q: Why does the geographic distance calculator use the Haversine formula instead of simple Pythagorean theorem? A: The Pythagorean theorem assumes a flat surface, but Earth is spherical. For distances over 20 km, Earth's curvature becomes significant. The Haversine formula calculates great-circle distances (shortest path on a sphere), which is essential for accurate geographic calculations.
Q: How many points can I add in multi-point mode? A: Technically, there's no hard limit, but practical performance considerations suggest keeping it under 50 points for optimal performance. The visualization remains clear, and calculations remain instantaneous for reasonable numbers of points.
Q: Can I use different units in the same calculation? A: No, you must use consistent units throughout a calculation. If you enter coordinates in meters, the distance will be in meters. The calculator doesn't perform unit conversions—it assumes all inputs use the same unit system.
Q: How do I measure real-world coordinates for input? A: For 2D/3D: Use rulers, tape measures, or CAD software. For geographic: Use GPS devices, smartphone apps, or online maps. Professional surveying equipment provides highest accuracy for critical applications.
Q: What's the "Additional Information" section showing? A: This section shows supplementary calculations like midpoints, slopes, bearings, segment breakdowns, and other relevant metrics that provide context beyond the basic distance measurement.
Q: Can I save or export my calculations? A: The current version doesn't have built-in save/export functions, but you can take screenshots of the results. The step-by-step calculations are designed to be educational and can be copied manually if needed for documentation.
Q: Is the calculator suitable for professional engineering work? A: While the tool provides high accuracy and follows proper mathematical principles, critical engineering applications should use specialized software with additional validation, industry-specific adjustments, and professional review processes.
🚀 Your Distance Calculation Action Plan
For Students
- Learn basic formulas (2D, 3D, Haversine)
- Use calculator to check homework
- Study step-by-step explanations
- Practice with different coordinate systems
For Professionals
- Standardize measurement units across projects
- Use appropriate mode for available data
- Document calculations with screenshot evidence
- Verify critical calculations with alternative methods
For DIY Projects
- Measure accurately with proper tools
- Add safety margins to calculations
- Use visualization to plan before implementation
- Double-check before cutting/building
Quick Calculation Steps
- Select calculation mode (4 options)
- Enter coordinate values
- Click Calculate
- Review visualization and results
- Study calculation steps
Common Scenarios
Room layout: Use 2D mode with consistent units Drone flight: Use 3D mode for altitude considerations Road trip: Use geographic mode for city distances Garden path: Use multi-point mode for curved paths Furniture arrangement: Use 2D mode with scale drawings
Essential Tools
- Distance Calculator - Your calculation tool
- Measuring tape/laser measure - For physical measurements
- GPS device/app - For geographic coordinates
- Notebook - For recording measurements
- Unit converter - If working with multiple unit systems
📏 Ready to Master Distance Calculations?
You now understand:
- Four different distance calculation methods
- Mathematical formulas and their applications
- Real-world applications across industries
- How to use our calculator effectively
- Tips for accurate measurements and calculations
Start calculating today:
- Open the Distance Calculator
- Select your calculation mode from four options
- Enter your coordinates accurately
- Get comprehensive results with visualizations
Remember: Whether you're a student learning geometry, an engineer designing structures, a traveler planning routes, or a DIY enthusiast tackling projects, our Distance Calculator is here to make your work more accurate, efficient, and understandable.
Happy calculating! 📐
Disclaimer: This calculator provides mathematical calculations for educational and planning purposes. While we strive for accuracy, always double-check critical measurements and consult professionals for important projects. The calculator assumes ideal conditions and may not account for terrain variations, obstacles, or other practical considerations in real-world applications.