Complete Area Calculator Guide: Master Geometry Calculations
Introduction: The Essential Geometry Tool
From home renovation projects to academic assignments, calculating area and perimeter is a fundamental skill that everyone needs. Our Area Calculator makes these calculations effortless, accurate, and educational. This comprehensive guide will help you understand how to use our calculator effectively and learn the mathematical principles behind area and perimeter calculations.
This guide will teach you:
- The fundamental concepts of area and perimeter
- Formulas for 8 common geometric shapes
- How to use our calculator for any shape
- Real-world applications of area calculations
- Tips for accurate measurements and calculations
Ready to calculate? Use our Area Calculator for instant calculations with step-by-step explanations.
📖 Table of Contents
- What Are Area and Perimeter?
- Why Area Calculations Matter in Real Life
- Square: The Foundation Shape
- Rectangle: The Most Common Shape
- Circle: Working with π
- Triangle: Three-Sided Calculations
- Rhombus: The Diamond Shape
- Trapezoid: The Slanted Shape
- Pentagon & Hexagon: Regular Polygons
- How to Use the Area Calculator
- Measurement Units Explained
- Common Calculation Mistakes to Avoid
- Real-World Applications
- Geometry Formulas Reference
- Tips for Accurate Measurements
- Converting Between Units
- Educational Benefits for Students
- Professional Uses
- FAQs: Your Geometry Questions Answered
- Practice Problems with Solutions
1️⃣ What Are Area and Perimeter?
Fundamental Definitions
Area: The amount of two-dimensional space inside a shape
- Measured in square units (cm², m², in², ft²)
- Represents surface coverage
- Used for: painting, flooring, land measurement
Perimeter: The total distance around a shape
- Measured in linear units (cm, m, in, ft)
- Represents boundary length
- Used for: fencing, trim, framing
Key Differences
| Aspect | Area | Perimeter |
|---|---|---|
| What it measures | Inside space | Outside boundary |
| Units | Square units | Linear units |
| Real-world use | How much material needed | How much edging needed |
| Formula type | Multiplication-based | Addition-based |
The Relationship
Important: Two shapes can have the same area but different perimeters, or same perimeter but different areas.
Example:
- A 4×4 square: Area = 16, Perimeter = 16
- A 2×8 rectangle: Area = 16, Perimeter = 20
Same area, different perimeter!
Why Both Matter
Complete projects require both calculations:
- Gardening: Area for soil, perimeter for fencing
- Construction: Area for flooring, perimeter for baseboards
- Manufacturing: Area for material, perimeter for cutting
The tool provides both automatically.
2️⃣ Why Area Calculations Matter in Real Life
Everyday Applications
Home Improvement:
- Flooring: Calculate carpet, tile, or wood needed
- Painting: Determine paint quantity for walls
- Landscaping: Plan garden beds, lawn areas
- Wallpaper: Estimate rolls required
Professional Uses:
- Construction: Material estimation
- Architecture: Space planning
- Manufacturing: Material optimization
- Agriculture: Field planning, irrigation
- Real Estate: Property valuation
Financial Implications
Area calculations affect costs:
- Materials are priced per square unit
- Labor often charges per area covered
- Property values based on square footage
- Tax assessments use area measurements
Planning and Design
Effective planning requires accurate area calculations:
- Furniture arrangement
- Room proportions
- Storage solutions
- Traffic flow
- Building codes compliance
Educational Value
Learning area calculations develops:
- Mathematical thinking
- Spatial reasoning
- Problem-solving skills
- Real-world math application
- Measurement accuracy
The interface makes these practical applications accessible to everyone.
3️⃣ Square: The Foundation Shape
Square Properties
Definition: A quadrilateral with four equal sides and four right angles All sides equal All angles = 90° Diagonals equal and perpendicular
Square Formulas
Area Formula:
A = s²
Where: s = side length
Perimeter Formula:
P = 4s
Diagonal Formula:
d = s√2 ≈ s × 1.414
Example Calculation
Square with side 5 cm:
Area = 5² = 25 cm²
Perimeter = 4 × 5 = 20 cm
Diagonal = 5 × √2 ≈ 7.07 cm
Real-World Squares
Common square objects:
- Floor tiles
- Chessboard squares
- Photo frames
- Windows
- Table tops
Using the Calculator for Squares
Simply enter: Side length Get automatically: Area, perimeter, diagonal Step-by-step explanation: Shows formula application
Special Properties
Squares are also:
- Rectangles (special case)
- Rhombuses (special case)
- Regular quadrilaterals
- The most symmetric quadrilateral
4️⃣ Rectangle: The Most Common Shape
Rectangle Properties
Definition: A quadrilateral with four right angles Opposite sides equal All angles = 90° Diagonals equal but not perpendicular
Rectangle Formulas
Area Formula:
A = l × w
Where: l = length, w = width
Perimeter Formula:
P = 2(l + w)
Diagonal Formula:
d = √(l² + w²)
Example Calculation
Rectangle with length 8 m, width 3 m:
Area = 8 × 3 = 24 m²
Perimeter = 2(8 + 3) = 22 m
Diagonal = √(8² + 3²) = √(64 + 9) = √73 ≈ 8.54 m
Real-World Rectangles
Everywhere around us:
- Doors and windows
- Rooms and buildings
- Paper sizes (A4, Letter)
- Screens (TV, monitor, phone)
- Books and tablets
Using the Calculator for Rectangles
Enter: Length and width Get: Area, perimeter, diagonal Visualization: Shows proper dimension labeling
The Golden Rectangle
Special ratio:
l/w = φ ≈ 1.618 (Golden Ratio)
Found in: Architecture, art, nature Considered aesthetically pleasing
Square as Special Rectangle
When l = w, rectangle becomes square All rectangle formulas work for squares
5️⃣ Circle: Working with π
Circle Properties
Definition: All points equidistant from center Constant radius from center Diameter = 2 × radius Circumference = distance around
Circle Formulas
Area Formula:
A = πr²
Where: r = radius, π ≈ 3.14159
Circumference (Perimeter) Formula:
C = 2πr = πd
Where: d = diameter
Diameter Formula:
d = 2r
The Magic of π (Pi)
π = Circumference ÷ Diameter Always constant for any circle Approximately 3.1415926535... Irrational number (infinite non-repeating decimal)
Example Calculation
Circle with radius 7 cm:
Area = π × 7² = π × 49 ≈ 153.94 cm²
Circumference = 2 × π × 7 ≈ 43.98 cm
Diameter = 2 × 7 = 14 cm
Real-World Circles
Circular objects:
- Wheels and tires
- Plates and cups
- Clocks and watches
- Pizzas and cakes
- Pipes and tubes
Using the Calculator for Circles
Enter: Radius (or diameter) Get: Area, circumference, diameter π precision: Uses high-precision calculation Visualization: Shows radius and diameter
Sector and Segment
Partial circle calculations:
- Sector: Pizza slice (area = (θ/360) × πr²)
- Segment: Chord area
- Annulus: Ring area
The tool focuses on full circles.
6️⃣ Triangle: Three-Sided Calculations
Triangle Properties
Definition: Three-sided polygon Three angles sum to 180° Various types: equilateral, isosceles, scalene Can be right-angled or oblique
Triangle Formulas
Area (using base and height):
A = ½ × b × h
Where: b = base, h = height (perpendicular)
Perimeter Formula:
P = a + b + c
Where: a, b, c are three sides
Heron's Formula (three sides known):
s = (a + b + c)/2 (semi-perimeter)
A = √[s(s-a)(s-b)(s-c)]
Example Calculation
Triangle with base 10 cm, height 6 cm:
Area = ½ × 10 × 6 = 30 cm²
Triangle with sides 5, 12, 13 cm:
Perimeter = 5 + 12 + 13 = 30 cm
s = 30/2 = 15
Area = √[15(15-5)(15-12)(15-13)] = √[15×10×3×2] = √900 = 30 cm²
Triangle Types
By sides:
- Equilateral: All sides equal, all angles 60°
- Isosceles: Two sides equal
- Scalene: All sides different
By angles:
- Acute: All angles < 90°
- Right: One angle = 90°
- Obtuse: One angle > 90°
Real-World Triangles
Structural uses:
- Roof trusses
- Bridge supports
- Shelf brackets
- Sign supports
Natural triangles:
- Mountain peaks
- Crystal formations
- Leaf arrangements
Using the Calculator for Triangles
Enter: Base and height (required) Optional: Other sides for perimeter Get: Area and (if sides provided) perimeter Multiple methods: Base-height or three sides
Right Triangle Special Case
Pythagorean Theorem:
a² + b² = c² (c = hypotenuse)
Area simpler: ½ × (leg1 × leg2)
7️⃣ Rhombus: The Diamond Shape
Rhombus Properties
Definition: Equilateral parallelogram All sides equal Opposite angles equal Diagonals perpendicular and bisect each other
Rhombus Formulas
Area (using diagonals):
A = ½ × d₁ × d₂
Where: d₁, d₂ are diagonal lengths
Area (using base and height):
A = b × h (like parallelogram)
Perimeter Formula:
P = 4s
Where: s = side length
Example Calculation
Rhombus with diagonals 10 cm and 6 cm:
Area = ½ × 10 × 6 = 30 cm²
Side = ½√(10² + 6²) = ½√(100 + 36) = ½√136 ≈ 5.83 cm
Perimeter = 4 × 5.83 ≈ 23.32 cm
Relationship to Other Shapes
Rhombus is a:
- Parallelogram (special case)
- Kite (special case)
- Square when angles = 90°
Real-World Rhombuses
Common examples:
- Diamond shapes (playing cards, jewelry)
- Traffic warning signs
- Kite designs
- Tile patterns
- Crystal structures
Using the Calculator for Rhombus
Enter: Both diagonals (required for area) Optional: Side for perimeter Get: Area and perimeter Automatic side calculation from diagonals
Special Properties
Diagonals bisect angles Diagonals perpendicular Area maximum when it's a square
8️⃣ Trapezoid: The Slanted Shape
Trapezoid Properties
Definition: Quadrilateral with one pair of parallel sides Parallel sides = bases Non-parallel sides = legs Height = perpendicular distance between bases
Trapezoid Formulas
Area Formula:
A = ½ × (b₁ + b₂) × h
Where: b₁, b₂ = parallel bases, h = height
Perimeter Formula:
P = b₁ + b₂ + l₁ + l₂
Where: l₁, l₂ = non-parallel sides
Example Calculation
Trapezoid with bases 12 cm, 8 cm, height 5 cm:
Area = ½ × (12 + 8) × 5 = ½ × 20 × 5 = 50 cm²
With legs 4 cm and 6 cm:
Perimeter = 12 + 8 + 4 + 6 = 30 cm
Trapezoid Types
Isosceles Trapezoid:
- Legs equal
- Base angles equal
- Symmetrical
Right Trapezoid:
- One leg perpendicular to bases
- Contains two right angles
Scalene Trapezoid:
- No special properties
Real-World Trapezoids
Practical applications:
- Roadway sections
- Building foundations
- Desk or table designs
- Dam cross-sections
- Architectural features
Using the Calculator for Trapezoid
Enter: Both bases and height (required) Optional: Legs for perimeter Get: Area and (if legs provided) perimeter Visualization: Shows base and height clearly
Special Case: Parallelogram
When b₁ = b₂, trapezoid becomes parallelogram Formula reduces to A = b × h
9️⃣ Pentagon & Hexagon: Regular Polygons
Regular Polygon Properties
Definition: All sides equal, all angles equal Pentagon: 5 sides Hexagon: 6 sides Apothem = perpendicular from center to side
Pentagon Formulas
Regular Pentagon (side s):
Area = (1/4)√(25 + 10√5) × s² ≈ 1.72048 × s²
Perimeter = 5s
Interior angle = 108°
Hexagon Formulas
Regular Hexagon (side s):
Area = (3√3/2) × s² ≈ 2.59808 × s²
Perimeter = 6s
Interior angle = 120°
Example Calculations
Pentagon with side 4 cm:
Area ≈ 1.72048 × 4² ≈ 27.53 cm²
Perimeter = 5 × 4 = 20 cm
Hexagon with side 3 cm:
Area ≈ 2.59808 × 3² ≈ 23.38 cm²
Perimeter = 6 × 3 = 18 cm
Real-World Pentagons & Hexagons
Pentagon examples:
- The Pentagon building
- Soccer ball panels
- Some flowers
- Military insignia
Hexagon examples:
- Honeycomb cells
- Bolts and nuts
- Turtle shells
- Snowflakes
- Basalt columns
Using the Calculator for Polygons
Enter: Side length Get: Area and perimeter Precise constants: Uses exact mathematical constants Visualization: Shows regular polygon shape
Why These Constants?
Derived from geometry:
- Split into triangles
- Use trigonometry
- Calculate apothem
- Sum triangle areas
The tool handles the complex math for you.
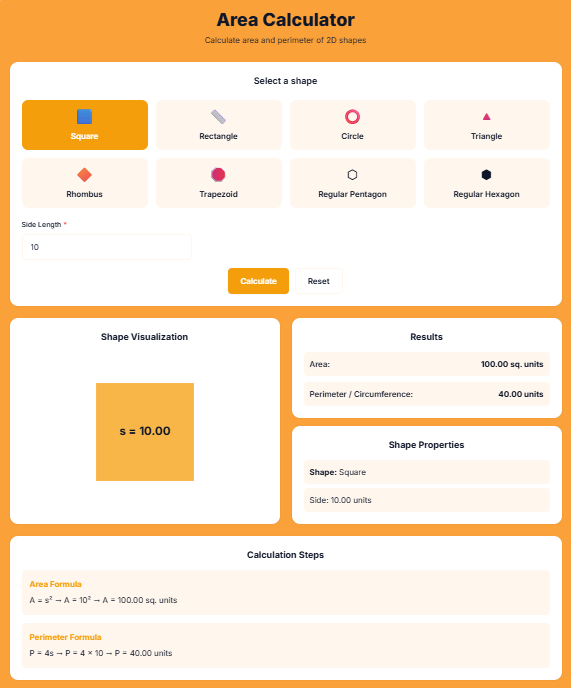
🔟 How to Use the Area Calculator
Step-by-Step Guide
Step 1: Select Shape
- Click on shape icon
- 8 shapes available
- Visual selection with emojis
Step 2: Enter Measurements
- Required fields marked with *
- Optional fields for perimeter
- Use decimal numbers
- Units don't matter (consistent)
Step 3: Calculate
- Click Calculate button
- Instant results
- Step-by-step explanation
Step 4: Interpret Results
- Area in square units
- Perimeter in linear units
- Shape visualization
- Formula steps
Input Tips
For accurate results:
- Measure carefully
- Use same units throughout
- Enter decimals for precision
- Don't mix units
- Check measurements twice
Common input formats:
- Whole numbers: 5, 10, 15
- Decimals: 3.5, 7.25, 12.75
- Fractions: Convert to decimals first
Shape Visualization
The tool shows:
- Shape diagram
- Dimension labels
- Measured values
- Clear representation
Helps verify you're measuring the right dimensions.
Step-by-Step Calculations
Educational feature:
- Shows formula used
- Substitutes your values
- Shows intermediate steps
- Provides final answer
Learn while calculating!
Reset Function
Clear all inputs with Reset button Start fresh with new shape Useful for multiple calculations
1️⃣1️⃣ Measurement Units Explained
Common Unit Systems
Metric System:
- Length: mm, cm, m, km
- Area: mm², cm², m², hectare, km²
Imperial System:
- Length: in, ft, yd, mi
- Area: in², ft², yd², acre, mi²
Choosing Units
Consider:
- What you're measuring
- Standard in your field
- Calculator/precision needed
- Personal preference
The interface works with any units (just be consistent).
Unit Conversions
Common conversions:
1 m = 100 cm
1 cm = 10 mm
1 ft = 12 in
1 yd = 3 ft
1 m² = 10,000 cm²
1 ft² = 144 in²
1 acre = 43,560 ft²
1 hectare = 10,000 m²
Precision in Measurements
How many decimals?
- Construction: Usually 0.01 units
- Crafting: Often 0.001 units
- Estimation: Whole numbers fine
- The calculator: Handles any precision
Real-World Unit Examples
When to use which:
- mm: Small parts, precision work
- cm: Everyday objects
- m: Rooms, buildings
- km: Land, roads
- in: US construction, crafts
- ft: US real estate, height
Choose units that make sense for your application.
1️⃣2️⃣ Common Calculation Mistakes to Avoid
Mistake 1: Wrong Dimensions
Measuring wrong dimension for formula Example: Using slant height instead of perpendicular height for triangle
Solution: Understand what each dimension represents in formulas.
Mistake 2: Unit Mixing
Using different units in same calculation Example: Length in cm, width in m
Solution: Convert all to same unit before calculating.
Mistake 3: Formula Misapplication
Using wrong formula for shape Example: Using rectangle formula for parallelogram without height
Solution: Know shape properties and required measurements.
Mistake 4: Calculator Errors
Input errors:
- Decimal point mistakes
- Negative values
- Missing required fields
Solution: Double-check entries before calculating.
Mistake 5: Perimeter vs. Area Confusion
Using wrong concept for application Example: Buying paint based on perimeter instead of area
Solution: Understand what each measures and when to use.
Mistake 6: Forgetting Conversions
Area conversions different from length Example: Thinking 100 cm² = 1 m² (actually 10,000 cm² = 1 m²)
Solution: Learn area conversion factors.
Mistake 7: Estimation Errors
Rounding too early in calculations Example: Rounding π to 3, then multiplying
Solution: Keep full precision until final answer, then round.
Built-in Safeguards
Automatic checks:
- Validates inputs
- Ensures positive dimensions
- Checks required fields
- Provides correct formulas
Still, understand the concepts behind calculations.
1️⃣3️⃣ Real-World Applications
Home Improvement Projects
Painting a room:
- Calculate wall area (excluding windows/doors)
- Multiply by coats needed
- Check paint coverage (m²/L)
- Add 10% for waste
Laying flooring:
- Calculate room area
- Add 5-10% for cutting waste
- Consider pattern matching
- Check tile/board dimensions
Gardening and Landscaping
Lawn area: For seeding/sodding Garden beds: For soil/compost Fencing: Perimeter for materials Paving: Area for stones/gravel
Construction and Renovation
Material estimation:
- Drywall sheets
- Roofing materials
- Insulation
- Siding
- Concrete
Cost estimation:
- Material costs per unit area
- Labor costs per unit area
- Total project budgeting
Academic and Professional
Students: Homework, projects, exams Teachers: Lesson planning, worksheets Engineers: Design calculations Architects: Space planning Designers: Material specifications
Everyday Decisions
Buying materials: Right quantities Space planning: Furniture arrangement Decorating: Rug/carpet sizes Storage: Shelf/bin capacities
Professional Application Tips
Save time on repetitive calculations Reduce errors in manual calculations Document calculations with step-by-step Share results easily
1️⃣4️⃣ Geometry Formulas Reference
Quick Formula Cheat Sheet
Square:
- Area: s²
- Perimeter: 4s
Rectangle:
- Area: l × w
- Perimeter: 2(l + w)
Circle:
- Area: πr²
- Circumference: 2πr
Triangle:
- Area: ½bh
- Perimeter: a + b + c
Rhombus:
- Area: ½d₁d₂
- Perimeter: 4s
Trapezoid:
- Area: ½(b₁ + b₂)h
- Perimeter: b₁ + b₂ + l₁ + l₂
Regular Pentagon:
- Area: ≈1.72048s²
- Perimeter: 5s
Regular Hexagon:
- Area: ≈2.59808s²
- Perimeter: 6s
Formula Derivations
Why these formulas work:
- Area formulas: Based on unit squares or triangle decomposition
- Perimeter formulas: Sum of side lengths
- Circle formulas: Derived from π definition
Understanding derivations helps remember formulas.
When Formulas Overlap
Some shapes are special cases:
- Square = Rectangle with l = w
- Square = Rhombus with 90° angles
- Parallelogram = Trapezoid with b₁ = b₂
Use simplest formula for given information.
Advanced Formulas
For irregular shapes:
- Composite shapes: Break into regular parts
- Coordinate geometry: Use vertices coordinates
- Integration: For curved boundaries
The tool focuses on regular shapes.
Formula Memory Tips
Mnemonic devices:
- "Area of rectangle is length times width"
- "Circle area is pi r squared" (pie are squared)
- "Triangle area is half base times height"
Practice with the calculator reinforces memory.
1️⃣5️⃣ Tips for Accurate Measurements
Measuring Tools
Essential tools:
- Tape measure (flexible)
- Ruler (straight edge)
- Laser measure (long distances)
- Calipers (precision)
- Measuring wheel (large areas)
Technique Matters
For straight lines:
- Keep tape straight
- Avoid sagging
- Measure at object height
- Use helper for long distances
For curves:
- Use flexible tape
- Follow contour
- Mark start/end points
- Consider string method
Multiple Measurements
Always measure twice!
- Reduces errors
- Catches mistakes
- Improves accuracy
Take several measurements and average if needed.
Dealing with Obstacles
Measuring around:
- Furniture
- Fixtures
- Irregular features
Break into sections and sum.
Recording Measurements
Good practice:
- Label clearly
- Include units
- Note date/time
- Sketch diagram
- Record conditions
The tool helps organize measurements.
Common Pitfalls
Avoid:
- Stretched tapes
- Bent rulers
- Parallax errors
- Temperature effects
- End point confusion
Be systematic and careful.
Digital Advantages
The interface provides:
- No manual calculation errors
- Step verification
- Visualization
- Memory of calculations
Still need accurate physical measurements.
1️⃣6️⃣ Converting Between Units
Why Conversion Matters
Materials sold in specific units Plans may use different units International projects need conversion Personal preference for units
Length Conversions
Metric:
1 km = 1000 m
1 m = 100 cm
1 cm = 10 mm
Imperial:
1 mi = 5280 ft
1 yd = 3 ft
1 ft = 12 in
Metric-Imperial:
1 in = 2.54 cm
1 ft = 30.48 cm
1 m = 3.28084 ft
Area Conversions
Critical: Area conversions are squares of length conversions!
Example:
1 m = 100 cm
But: 1 m² = 10,000 cm² (100²)
Common area conversions:
1 m² = 10.7639 ft²
1 ft² = 929.03 cm²
1 acre = 4046.86 m²
1 hectare = 2.47105 acres
Conversion Strategy
Best approach:
- Convert all measurements to one system
- Calculate area/perimeter
- Convert result if needed
Avoid: Converting area formulas directly.
Unit-Agnostic Approach
The calculator is:
- Use any units
- Just be consistent
- Result in same square units
Example: Enter cm, get cm²; enter ft, get ft².
When Precision Matters
Construction: Usually 2-3 decimal places Land survey: May need more precision Crafting: Often millimeter precision
High precision is handled.
Conversion Tools
Built-in conversion: Not needed with this approach Separate converters: Available online Smartphone apps: Quick conversions
Simplest: Stick to one unit system.
1️⃣7️⃣ Educational Benefits for Students
Learning Geometry Concepts
Visual understanding:
- Shape recognition
- Dimension relationships
- Formula visualization
- Spatial reasoning
Interactive visualization enhances learning.
Formula Application Practice
See formulas in action:
- Input values
- See substitution
- Watch calculation steps
- Verify results
Active learning vs. memorization.
Problem-Solving Skills
Develops:
- Logical thinking
- Step-by-step approach
- Verification habits
- Error checking
Real-world context makes math meaningful.
Multiple Learning Styles
Visual learners: Shape diagrams Auditory learners: Step explanations Kinesthetic learners: Input interaction Reading/writing: Text explanations
All styles are accommodated.
Homework Assistance
Check work:
- Verify calculations
- Understand mistakes
- Learn correct approach
- Build confidence
Not for cheating, for learning!
Test Preparation
Practice problems:
- Various shapes
- Different measurements
- Mixed units
- Real-world scenarios
Build fluency with calculations.
Teacher Resource
Create worksheets with examples Demonstrate concepts visually Generate practice problems Show real applications
Enhance classroom teaching.
STEM Foundation
Geometry is foundation for:
- Physics
- Engineering
- Architecture
- Computer graphics
- Design
Early mastery supports future learning.
1️⃣8️⃣ Professional Uses
Construction Industry
Quantity surveying:
- Material takeoffs
- Cost estimation
- Bid preparation
- Project planning
Save time on repetitive calculations.
Architecture and Design
Space planning:
- Room layouts
- Furniture arrangement
- Traffic flow
- Building codes compliance
Accurate calculations prevent costly mistakes.
Manufacturing
Material optimization:
- Minimize waste
- Calculate yields
- Pattern layout
- Cost analysis
Small improvements in accuracy yield big savings.
Real Estate
Property assessment:
- Square footage
- Lot size
- Building area
- Valuation
Accurate measurements affect property value.
Landscaping
Project planning:
- Lawn area
- Garden beds
- Paving
- Fencing
Right quantities prevent waste or shortage.
Education Sector
Teaching tool:
- Math classes
- Vocational training
- Adult education
- Online courses
Makes abstract concepts concrete.
DIY and Home Improvement
Weekend projects:
- Painting
- Flooring
- Tiling
- Gardening
Professional results with amateur skills.
Quality Assurance
Verification tool:
- Check contractor calculations
- Verify material orders
- Audit project estimates
- Ensure compliance
Independent verification builds trust.
❓ Frequently Asked Questions
Q: How accurate is the area calculator? A: The tool uses precise mathematical formulas and high-precision calculations (typically 10+ decimal places). The accuracy of your results depends entirely on the accuracy of your input measurements. Calculations are performed with much higher precision than typically needed, then rounded to 2 decimal places for display.
Q: Can I use the calculator for irregular shapes? A: The interface is designed for regular geometric shapes. For irregular shapes, you need to break them down into regular components (triangles, rectangles, etc.), calculate each area separately, then sum them. The focus is on the 8 most common regular shapes that cover most practical needs.
Q: What units should I use? A: You can use any units (cm, m, inches, feet, etc.) as long as you're consistent. If you enter measurements in centimeters, the area will be in square centimeters. If you enter feet, area will be in square feet. The calculator doesn't convert units—it assumes all inputs are in the same unit system.
Q: Why does the triangle calculator need height, not just sides? A: For area calculation, triangles require base and perpendicular height. If you only have three sides, you can use Heron's formula, but the calculator uses the simpler base-height method for most users. For perimeter, all three sides are needed.
Q: How do I measure the height of a triangle? A: The height (altitude) is the perpendicular distance from the base to the opposite vertex. It's not necessarily one of the sides unless it's a right triangle. Use a right angle tool or measure the vertical distance if the triangle is drawn to scale.
Q: Can I calculate the area of a circle if I only know the diameter? A: Yes! The radius is half the diameter. If you know diameter (d), use radius = d/2 in the calculator. Or remember: Area = π(d/2)² = (πd²)/4.
Q: What's the difference between perimeter and circumference? A: Perimeter is the total distance around any polygon. Circumference is specifically the distance around a circle. They're conceptually the same (boundary length) but use different formulas. The calculator uses "perimeter" for polygons and "circumference" for circles.
Q: Why are there constants like 1.72048 for pentagon area? A: These constants come from the geometry of regular polygons. For a regular pentagon with side s, the area formula is (1/4)√(25+10√5)s², which simplifies to approximately 1.72048s². These precise constants ensure accurate calculations.
Q: Can I save my calculations? A: The current version doesn't have a save function, but you can take screenshots or note down the results. For multiple calculations, you might want to record them in a spreadsheet or notebook along with your measurements.
Q: Is this calculator suitable for school assignments? A: Yes, but check your teacher's policy on calculator use. The tool is excellent for checking your work, understanding steps, and learning concepts. It shouldn't replace learning how to do the calculations manually, but it's a great learning aid.
🚀 Your Area Calculation Action Plan
For Home Projects
- Measure carefully with proper tools
- Use the calculator for each shape component
- Add 5-10% waste for materials
- Double-check before purchasing
For Students
- Learn formulas first
- Use calculator to check work
- Study step-by-step explanations
- Practice with different shapes
For Professionals
- Standardize measurements in one unit system
- Use calculator for quick estimates
- Document calculations for reference
- Verify critical calculations manually
Quick Reference Steps
- Select shape from 8 options
- Enter measurements (required fields marked *)
- Click Calculate for instant results
- Review steps to understand calculation
- Use results for your project
Common Scenarios
Painting a room: Calculate wall area, subtract windows/doors Laying tile: Calculate floor area, add cutting waste Building fence: Calculate perimeter for linear materials Gardening: Calculate area for soil/seed/fertilizer
Tools You'll Need
- Area Calculator - Your calculation tool
- Measuring tape - For accurate measurements
- Notebook - For recording measurements
- Pencil/pen - For sketches and notes
- Unit converter (if mixing units)
📐 Ready to Calculate Any Shape?
You now understand:
- How to calculate area and perimeter for 8 common shapes
- Why these calculations matter in real life
- How to use our calculator effectively
- Tips for accurate measurements and calculations
Start calculating today:
- Open the Area Calculator
- Select your shape from the visual menu
- Enter your measurements accurately
- Get instant results with step-by-step explanations
Remember: Whether you're a student learning geometry, a DIY enthusiast tackling home projects, or a professional needing quick calculations, our Area Calculator is here to make your work easier, faster, and more accurate.
Happy calculating! 📏✨
Disclaimer: This calculator provides mathematical calculations for educational and planning purposes. While we strive for accuracy, always double-check critical measurements and consult professionals for important projects. The calculator assumes standard geometric shapes and may not account for irregularities, waste, or other practical considerations in real-world applications.