Complete Circle Calculator Guide: Master Circle Geometry
Introduction: The Perfect Shape
The circle is one of the most fundamental and perfect shapes in mathematics and nature. From engineering to astronomy, understanding circle properties is essential. Our Circle Calculator makes these calculations effortless, providing accurate results with visual representations and step-by-step explanations.
This guide will teach you:
- All circle formulas and their derivations
- Six different calculation methods
- Real-world applications of circle calculations
- How to use our calculator effectively
- Tips for accurate measurements and calculations
Ready to calculate? Use our Circle Calculator for comprehensive circle calculations with visualizations.
📖 Table of Contents
- The Circle: Nature's Perfect Shape
- Six Calculation Methods Explained
- Radius: The Fundamental Measurement
- Diameter: Twice the Radius
- Circumference: The Circle's Perimeter
- Area: The Space Inside
- Arc Length: Partial Circumference
- Sector Area: Pie Slice Calculations
- Circle Calculator: Step-by-Step Guide
- Interactive Visualization Features
- The Magic of π (Pi)
- Real-World Applications
- Common Circle Calculation Mistakes
- Measurement Units and Conversions
- Advanced Circle Properties
- Related Circle Calculations
- Educational Benefits
- Professional Uses
- FAQs: Your Circle Questions Answered
- Practice Problems with Solutions
1️⃣ The Circle: Nature's Perfect Shape
Definition and Properties
Definition: A set of all points equidistant from a center point Key properties:
- Constant curvature
- Infinite lines of symmetry
- No beginning or end
- Perfectly round
Why Circles Are Everywhere
Natural circles:
- Planets and stars
- Ripples in water
- Tree rings
- Eyes and pupils
- Bubbles and droplets
Human-made circles:
- Wheels and gears
- Clocks and watches
- Coins and buttons
- Plates and cups
- Manhole covers
Mathematical Significance
Circles represent:
- Perfection in geometry
- Constant ratio (π)
- Basis for trigonometry
- Foundation for calculus
- Key in coordinate geometry
The tool helps you explore these properties.
Circle vs. Other Shapes
Unique features:
- Only shape with constant width
- Most efficient perimeter-to-area ratio
- Only shape that rolls smoothly
- Basis for spheres (3D circles)
2️⃣ Six Calculation Methods Explained
Multiple Entry Points
The calculator offers 6 ways to start calculations:
- Radius: From center to edge
- Diameter: Through the center
- Circumference: Distance around
- Area: Space inside
- Arc Length: Partial boundary
- Sector Area: Pie slice area
Why Multiple Methods?
Different situations require different inputs:
- Engineering: Often know diameter
- Construction: May measure circumference
- Design: Might specify area
- Manufacturing: Could work with arcs
The interface handles any starting point.
Method Selection Guide
Choose based on what you know:
- Radius: Simplest, most direct
- Diameter: Common in pipe/wheel specs
- Circumference: Measured with tape
- Area: For material calculations
- Arc/Sector: For partial circles
All methods give complete circle properties.
Input Validation
The tool checks:
- Positive values
- Valid angles (0-360°)
- Reasonable precision
- Mathematical validity
Prevents errors in calculations.
3️⃣ Radius: The Fundamental Measurement
What Is Radius?
Definition: Distance from center to any point on circle Symbol: r (lowercase) Key property: Constant for a given circle
Radius Formulas
From diameter:
r = d ÷ 2
From circumference:
r = C ÷ (2π)
From area:
r = √(A ÷ π)
From arc length:
r = L ÷ θ (θ in radians)
From sector area:
r = √(2A_s ÷ θ) (θ in radians)
Example Calculations
Given circumference 31.416 cm:
r = 31.416 ÷ (2 × 3.1416)
r = 31.416 ÷ 6.2832
r = 5 cm
Given area 78.54 cm²:
r = √(78.54 ÷ 3.1416)
r = √25
r = 5 cm
Real-World Radius Examples
Common measurements:
- Wheel radius (automotive)
- Lens radius (optics)
- Curve radius (roads)
- Turning radius (vehicles)
- Atomic radius (chemistry)
Using Radius in the Calculator
Direct input: Enter radius value Visualization: Shows radius line All calculations: Derive from radius
Radius is the foundation for all other properties.
4️⃣ Diameter: Twice the Radius
What Is Diameter?
Definition: Distance through center, connecting two points on circle Symbol: d (lowercase) Relationship: d = 2r
Diameter Formulas
From radius:
d = 2r
From circumference:
d = C ÷ π
From area:
d = 2√(A ÷ π)
Example Calculations
Given radius 7.5 cm:
d = 2 × 7.5 = 15 cm
Given circumference 47.124 cm:
d = 47.124 ÷ 3.1416 = 15 cm
Why Diameter Matters
Practical advantages:
- Easier to measure directly
- Common in specifications
- Used in manufacturing
- Standard in engineering drawings
Real-World Diameter Examples
Everyday measurements:
- Pipe diameters (plumbing)
- Bolt diameters (mechanical)
- Coin diameters (currency)
- Pizza diameters (food)
- Telescope diameters (astronomy)
Diameter vs. Radius
Diameter is often preferred because:
- Can be measured with calipers
- Doesn't require finding center
- More intuitive for many people
- Standard in industry specs
The tool works equally well with either.
5️⃣ Circumference: The Circle's Perimeter
What Is Circumference?
Definition: Distance around the circle Symbol: C (uppercase) Key formula: C = 2πr = πd
The π Connection
π (pi) = Circumference ÷ Diameter Always approximately 3.14159 Irrational number (infinite decimal)
Circumference Formulas
From radius:
C = 2πr
From diameter:
C = πd
From area:
C = 2√(πA)
Example Calculations
Given radius 10 cm:
C = 2 × π × 10 ≈ 62.832 cm
Given diameter 20 cm:
C = π × 20 ≈ 62.832 cm
Real-World Circumference
Practical applications:
- Tire sizes (automotive)
- Belt lengths (mechanical)
- Fencing circles (gardening)
- Wrist sizes (jewelry)
- Head circumference (medical)
Measuring Circumference
Direct measurement: Use flexible tape Indirect calculation: From radius/diameter The tool provides accurate values
Circumference in Nature
Natural circles have mathematically precise circumferences Tree rings show annual growth Planetary orbits involve circumference
6️⃣ Area: The Space Inside
What Is Circle Area?
Definition: Amount of 2D space enclosed by circle Symbol: A (uppercase) Key formula: A = πr²
Area Formulas
From radius:
A = πr²
From diameter:
A = (πd²) ÷ 4
From circumference:
A = C² ÷ (4π)
Example Calculations
Given radius 6 cm:
A = π × 6² = π × 36 ≈ 113.097 cm²
Given diameter 12 cm:
A = (π × 12²) ÷ 4 = (π × 144) ÷ 4 ≈ 113.097 cm²
Why Area Matters
Practical importance:
- Material calculations
- Coverage estimates
- Space planning
- Cost calculations
- Efficiency ratios
Real-World Area Examples
Common calculations:
- Paint needed for circular wall
- Pizza size comparisons
- Land area for circular plots
- Fabric for circular tablecloth
- Solar panel coverage
Area Units
Always square units:
- cm², m², in², ft²
- Conversion factors differ from linear units The calculator maintains proper units
Area vs. Circumference Relationship
Fixed ratio: For given perimeter, circle has maximum area This makes circles most efficient shape for enclosing area
7️⃣ Arc Length: Partial Circumference
What Is Arc Length?
Definition: Length of a portion of circumference Symbol: L (uppercase) Key formula: L = rθ (θ in radians)
Angle Measurement
Degrees vs. Radians:
- Degrees: 360 in full circle
- Radians: 2π in full circle
- Conversion: radians = degrees × (π/180)
Arc Length Formulas
Using degrees:
L = (θ ÷ 360) × 2πr
Using radians:
L = rθ
Example Calculations
Given radius 8 cm, angle 45°:
L = (45 ÷ 360) × 2π × 8
L = 0.125 × 50.265
L ≈ 6.283 cm
Using radians (π/4):
L = 8 × (π/4) = 2π ≈ 6.283 cm
Real-World Arc Applications
Practical uses:
- Road curves (civil engineering)
- Arch designs (architecture)
- Camera lenses (optics)
- Roller coaster tracks
- Clock hands movement
Measuring Arcs
Direct measurement: Challenging Calculation preferred: From radius and angle The tool simplifies arc calculations
Special Arc Cases
Semicircle: θ = 180°, L = πr Quarter circle: θ = 90°, L = (πr)/2 Additionally, you get these special cases
8️⃣ Sector Area: Pie Slice Calculations
What Is Sector Area?
Definition: Area of pie-slice portion of circle Symbol: A_s Key formula: A_s = (θ ÷ 360) × πr²
Sector Formulas
Using degrees:
A_s = (θ ÷ 360) × πr²
Using radians:
A_s = (1/2)r²θ
Example Calculations
Given radius 10 cm, angle 60°:
A_s = (60 ÷ 360) × π × 10²
A_s = (1/6) × π × 100
A_s ≈ 52.360 cm²
Real-World Sector Applications
Common uses:
- Pie chart segments (data visualization)
- Pizza slices (food service)
- Garden sections (landscaping)
- Window designs (architecture)
- Gear teeth (mechanical)
Sector vs. Segment
Sector: Includes center (pie slice) Segment: Excludes center (chord area) The interface focuses on sectors
Special Sector Cases
Semicircle: θ = 180°, A_s = (πr²)/2 Quarter circle: θ = 90°, A_s = (πr²)/4 These are provided automatically
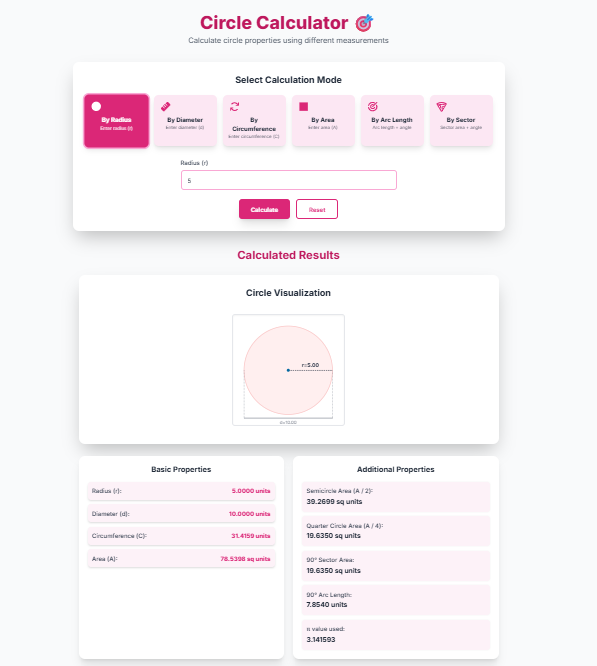
9️⃣ Circle Calculator: Step-by-Step Guide
Mode Selection
Six colorful options:
- Radius mode (pink): Direct radius input
- Diameter mode: Diameter measurement
- Circumference mode: Perimeter known
- Area mode: Space calculation
- Arc mode: Partial circumference
- Sector mode: Pie slice area
Input Entry
For each mode:
- Enter known value(s)
- Use decimal numbers
- Positive values only
- Appropriate units
Angle inputs: 0-360° for arc/sector modes
Calculation Process
Click "Calculate":
- Validates inputs
- Calculates radius first
- Derives all properties
- Generates step-by-step
- Creates visualization
Results Interpretation
Four result sections:
- Visualization: Interactive diagram
- Basic Properties: Radius, diameter, circumference, area
- Additional Properties: Semicircle, quarter circle, 90° sector/arc
- Calculation Steps: Detailed derivation
Reset Function
Soft reset: Clears inputs Keeps mode selection Ready for new calculation
Visualization Features
Interactive diagram shows:
- Circle with radius/diameter
- Arc/sector when applicable
- Angle measurements
- Dimension labels
Helps verify calculations visually.
🔟 Interactive Visualization Features
Live Circle Diagram
Dynamic visualization:
- Updates with calculations
- Shows current mode context
- Displays measured values
- Illustrates relationships
Mode-Specific Visuals
Each mode has unique display:
- Radius/Diameter: Shows linear dimensions
- Arc: Highlights arc segment
- Sector: Fills sector area
- All modes: Show radius line
Dimension Display
Clear labeling:
- Radius (r) value
- Diameter (d) value
- Angle when applicable
- Arc/sector highlights
Educational Value
Visual learning benefits:
- Understand relationships
- See formula applications
- Verify calculations
- Build spatial reasoning
Professional Utility
Design verification:
- Check proportions
- Validate measurements
- Communicate designs
- Present calculations
Responsive Design
Works on all devices:
- Desktop computers
- Tablets
- Smartphones
- Different screen sizes
Visualization adapts to your device.
1️⃣1️⃣ The Magic of π (Pi)
What Is π?
Mathematical constant: Ratio of circumference to diameter Approximately: 3.141592653589793... Irrational number: Infinite non-repeating decimal Transcendental number: Not root of any polynomial with integer coefficients
Historical Significance
Ancient discoveries:
- Babylonians: ≈3.125
- Egyptians: ≈3.1605
- Archimedes: 3.1408 < π < 3.1429
- Chinese mathematicians: Calculated to 7 digits
Modern Computation
Computer calculations:
- Trillions of digits known
- Continually refined
- Used in precision work
- The tool uses: 3.141592653589793
π in Formulas
Essential in circle calculations:
- Circumference: C = 2πr
- Area: A = πr²
- Arc length: L = rθ (θ in radians)
- Sector area: A_s = (1/2)r²θ
Why π Matters
Fundamental constant:
- Appears throughout mathematics
- Essential in physics
- Key in engineering
- Important in statistics
High-precision π is used throughout.
π Day Celebration
March 14 (3/14):
- Mathematical holiday
- Celebrate at 1:59 PM
- Relates to π ≈ 3.14159
1️⃣2️⃣ Real-World Applications
Engineering and Construction
Structural calculations:
- Arch designs
- Dome constructions
- Pipe systems
- Wheel and gear design
- Bridge curves
Manufacturing
Precision components:
- Bearings and bushings
- Gaskets and seals
- Lens production
- Tool design
- Mold making
Science and Research
Scientific applications:
- Planetary orbits
- Wave patterns
- Lens optics
- Fluid dynamics
- Statistical analysis
Everyday Life
Common calculations:
- Pizza size comparison
- Garden planning
- Sports field markings
- Round table measurements
- Clock and watch design
Digital Technology
Computer applications:
- Graphics rendering
- Game development
- Animation
- User interface design
- Data visualization
Using the Tool Professionally
Save time on repetitive calculations Reduce errors in manual work Document calculations with steps Share visualizations with teams
1️⃣3️⃣ Common Circle Calculation Mistakes
Mistake 1: Using Wrong π Value
Using 3.14 instead of more precise value Solution: High-precision π is built in
Mistake 2: Confusing Radius and Diameter
Using d instead of r in formulas Solution: Visualization shows both clearly
Mistake 3: Angle Unit Confusion
Using degrees in radian formulas Solution: The tool handles conversion
Mistake 4: Square Unit Errors
Forgetting to square radius in area Solution: Step-by-step shows correct formula
Mistake 5: Negative Values
Entering negative measurements Solution: Input validation prevents this
Mistake 6: Early Rounding
Rounding intermediate values Solution: Full precision is maintained
Mistake 7: Unit Mixing
Using different units in one calculation Solution: Use consistent units throughout
Built-in Safeguards
Prevention through:
- Input validation
- High-precision calculations
- Clear formulas
- Unit consistency
- Step verification
Still, understand the concepts.
1️⃣4️⃣ Measurement Units and Conversions
Common Unit Systems
Metric System:
- Length: mm, cm, m, km
- Area: mm², cm², m², hectare
Imperial System:
- Length: in, ft, yd, mi
- Area: in², ft², yd², acre
Choosing Units
Consider:
- Application requirements
- Industry standards
- Measurement tools available
- Personal preference
The tool works with any units (be consistent).
Unit Conversions
Length conversions:
1 m = 100 cm
1 cm = 10 mm
1 ft = 12 in
1 yd = 3 ft
Area conversions (critical):
1 m² = 10,000 cm² (100²)
1 ft² = 144 in² (12²)
1 m² ≈ 10.764 ft²
Precision Requirements
Different applications need different precision:
- Construction: Usually ±1 mm
- Manufacturing: Often ±0.01 mm
- Surveying: High precision needed
- Estimation: Round numbers acceptable
High precision is provided.
Unit Strategy
Best practice:
- Measure in convenient units
- Convert to calculation units
- Calculate
- Convert result if needed
The interface simplifies this process.
1️⃣5️⃣ Advanced Circle Properties
Circle Equations
Standard form:
(x - h)² + (y - k)² = r²
Center at (h, k), radius r
General form:
x² + y² + Dx + Ey + F = 0
Circle Theorems
Important theorems:
- Thales' theorem
- Inscribed angle theorem
- Tangent-secant theorem
- Chord-chord theorem
Circle in Coordinate Geometry
Distance formula application:
r = √[(x - h)² + (y - k)²]
Circle and Trigonometry
Parametric equations:
x = h + r cos θ
y = k + r sin θ
Advanced Calculations
Beyond basic calculator:
- Intersecting circles
- Tangent lines
- Circle packing
- Optimal positioning
The tool focuses on practical applications.
Circle in Calculus
Derivatives and integrals:
- Area derivation
- Arc length integration
- Volume of revolution
- Surface area calculations
1️⃣6️⃣ Related Circle Calculations
Annulus (Ring) Area
Area between two circles:
A = π(R² - r²)
R = outer radius, r = inner radius
Segment Area
Area between chord and arc:
A_segment = A_sector - A_triangle
Circumscribed Circle
Circle around polygon:
- Triangle circumcircle
- Regular polygon circumcircle
Inscribed Circle
Circle inside polygon:
- Triangle incircle
- Regular polygon incircle
Concentric Circles
Same center, different radii Common in engineering
Overlapping Circles
Area of intersection Complex calculation
Using the Tool as Foundation
Start with basic circle Build to complex shapes Understand relationships
1️⃣7️⃣ Educational Benefits
Learning Geometry Concepts
Visual understanding:
- Radius-diameter relationship
- Circumference-area connection
- Angle-arc proportion
- π significance
Interactive visualization enhances learning.
Formula Application
See formulas in action:
- Input values
- Watch calculations
- See step-by-step
- Verify results
Active learning vs. memorization.
Problem-Solving Skills
Develops:
- Logical thinking
- Step-by-step approach
- Verification habits
- Error checking
Real context makes math meaningful.
Multiple Learning Styles
Accommodates all learners:
- Visual: Diagrams and colors
- Auditory: Step explanations
- Kinesthetic: Interactive inputs
- Reading/writing: Detailed text
All styles are served.
Homework Assistance
Check work:
- Verify calculations
- Understand mistakes
- Learn correct approach
- Build confidence
Educational tool, not cheating.
Test Preparation
Practice problems:
- Various starting points
- Different units
- Real scenarios
- Timed practice
Build fluency with calculations.
Teacher Resource
Create lessons with examples Demonstrate concepts visually Generate practice problems Show real applications
Enhance classroom teaching.
1️⃣8️⃣ Professional Uses
Engineering Design
Mechanical engineering:
- Gear design
- Bearing calculations
- Pipe systems
- Machine components
Civil engineering:
- Road curves
- Arch structures
- Roundabout design
- Tunnel planning
Architecture
Building design:
- Dome constructions
- Circular rooms
- Window designs
- Rotunda planning
Manufacturing
Production planning:
- Material estimation
- Tool design
- Quality control
- Process optimization
Science and Research
Scientific applications:
- Optics calculations
- Wave analysis
- Orbital mechanics
- Statistical sampling
Construction
Practical applications:
- Circular foundations
- Pipe installations
- Tank construction
- Dome building
Digital Design
Computer graphics:
- UI design
- Game development
- Animation
- Data visualization
Professional Application Tips
Save time on calculations Reduce errors in work Document steps for reference Share results with teams
❓ Frequently Asked Questions
Q: How accurate is the circle calculator? A: The tool uses double-precision floating-point arithmetic with high-precision π (3.141592653589793). This provides accuracy to about 15 decimal places, which is far more precise than most practical applications require. The limiting factor is usually the accuracy of your input measurements, not the calculator's precision.
Q: Can I calculate a circle from just the circumference? A: Yes! Select "By Circumference" mode, enter the circumference value, and the calculator will determine the radius, then calculate all other properties. The formula used is: r = C ÷ (2π), where C is circumference and π is approximately 3.14159.
Q: What's the difference between arc length and sector area? A: Arc length is the distance along the circle's edge (like the crust of a pizza slice). Sector area is the area of the pie-slice shape (including the area inside the circle). Both require knowing the central angle, but arc length is a linear measurement while sector area is an area measurement.
Q: Why does the calculator convert degrees to radians? A: Radians are the natural unit for angle measurement in mathematics because they simplify many formulas. For arc length: L = rθ (θ in radians). For sector area: A = (1/2)r²θ (θ in radians). The tool handles the conversion automatically: θ(radians) = θ(degrees) × (π/180).
Q: Can I calculate only part of a circle? A: Yes, use either "Arc Length" or "Sector Area" mode. For arcs, enter the arc length and central angle. For sectors, enter the sector area and central angle. The calculator will determine the full circle's radius first, then give you all properties including the partial measurements.
Q: What units should I use? A: You can use any units (cm, inches, meters, feet, etc.) as long as you're consistent. If you enter radius in centimeters, the area will be in square centimeters. The calculator doesn't convert units—it assumes all inputs use the same unit system.
Q: How do I measure the diameter of a circular object? A: Use calipers for precision, or measure the circumference with a flexible tape and calculate diameter using: d = C/π. For large objects, measure across the center at the widest point. The tool can work from any of these measurements.
Q: What's the significance of the 90° calculations shown? A: 90° represents a quarter circle, which is a common angle in many applications (right angles, corners, quadrants). The calculator shows 90° sector area and 90° arc length because these are frequently needed in design, construction, and manufacturing.
Q: Can this calculator handle very large or very small circles? A: The calculator can handle a wide range of values, from microscopic (0.000001 units) to astronomical (1,000,000+ units). However, extremely large or small numbers may encounter JavaScript floating-point limitations, but these are well beyond practical measurement ranges.
Q: Is there a way to save or export my calculations? A: The current version doesn't have save/export functions, but you can take screenshots of the results. The step-by-step calculations are designed to be educational and can be copied manually if needed for documentation.
🚀 Your Circle Calculation Action Plan
For Students
- Learn basic formulas (C = 2πr, A = πr²)
- Use calculator to check homework
- Study step-by-step explanations
- Practice with different starting points
For Professionals
- Standardize measurement units
- Use appropriate mode for available data
- Document calculations with steps
- Verify critical calculations manually
For DIY Projects
- Measure accurately with proper tools
- Add safety margins to calculations
- Use visualization to plan
- Double-check before cutting/making
Quick Calculation Steps
- Select calculation mode (6 options)
- Enter known value(s)
- Click Calculate
- Review visualization and results
- Study calculation steps
Common Scenarios
Pipe installation: Use diameter mode Garden planning: Use area or circumference Arch design: Use arc or sector mode Wheel specifications: Use radius or diameter Material estimation: Use area calculations
Essential Tools
- Circle Calculator - Your calculation tool
- Measuring tape/ruler - For physical measurements
- Calipers - For precision diameter
- Notebook - For recording measurements
- Unit converter - If mixing unit systems
⭕ Ready to Master Circle Calculations?
You now understand:
- All circle formulas and their relationships
- Six different ways to calculate circle properties
- Real-world applications of circle mathematics
- How to use our calculator effectively
- Tips for accurate measurements and calculations
Start calculating today:
- Open the Circle Calculator
- Select your calculation mode from six options
- Enter your measurements accurately
- Get comprehensive results with visualizations
Remember: Whether you're a student learning geometry, an engineer designing components, an architect planning spaces, or a DIY enthusiast tackling projects, our Circle Calculator is here to make your work more accurate, efficient, and understandable.
Happy calculating! 🎯
Disclaimer: This calculator provides mathematical calculations for educational and planning purposes. While we strive for accuracy, always double-check critical measurements and consult professionals for important projects. The calculator assumes perfect circles and may not account for irregularities, tolerances, or other practical considerations in real-world applications.